Un peu plus de précision
En utilisant la technique mise en oeuvre à la page précédente, tu vas tracer quelques diagrammes du même type.
- Fonction f définie par f(x) = sin(x)*cos(x)
- Intervalle d'étude = [-π ; +π] (approximativement) avec un pas de 0,2. Pense à utiliser la fonction pi() où c'est possible.
- Variante de type de diagramme = Points et Lignes
- La légende indique la nature de la fonction étudiée
- Le titre du diagramme est Fonction trigonométrique
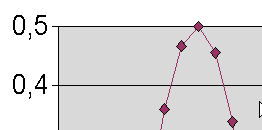Dites, c'est un peu n'importe quoi, ce
diagramme. Je n'avais jamais vu de fonction trigonométrique avec des
points anguleux. Regardez, je vous ai mis un agrandissement...
Vous avez parfaitement raison: ce diagramme n'est
pas correct.
Mais la faute réside dans la façon de travailler. La méthode doit être
un peu améliorée.
Dans l'étude de la fonction, nous avons choisi de calculer seulement une bonne trentaine de points répartis régulièrement sur l'intervalle d'étude.
Manuellement, nous tracerions spontanément une courbe entre les différents points calculés. Nous savons que ce diagramme doit être une courbe. Donc, nous idéalisons.
Le tableur relie ces points par des segments de droite, car il ne dispose d'aucun moyen de déterminer des valeurs intermédiaires.
Bien, je reprends donc mon crayon, ma calculette et mon papier millimétré ?
Il ne faut pas forcément jeter l'ordinateur à la poubelle, si nous sommes capables d'être intelligents à sa place.
Si l'on suspecte un diagramme mathématique de ne pas correspondre à la réalité, on peut pousser l'analyse plus loin. Dans le cas présent, augmenter le nombre de points calculés serait une bonne option.
Re-dessine le diagramme de la fonction f
avec f(x) = sin(x) * cos(x)
- dans le même intervalle, mais
- en utilisant un pas de 0,05. On calcule ainsi près de 130 valeurs de f(x).
- Sélectionne la variante Lignes Seules du type XY Dispersion
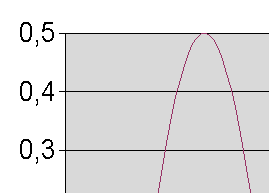
Vérifie que les points anguleux ont disparu au
profit d'une courbe bien lisse, comme sur l'illustration ci-contre.
La variante Uniquement lignes
permet d'augmenter la clarté du diagramme qui serait trop encombré par
le grand nombre de symboles 
correspondant
chacun à un point calculé.
Bien, on va donc toujours calculer un maximum de points et utiliser la variante Lignes Seules pour éviter les soucis.
Ce n'est pas forcément toujours nécessaire. Dans certains cas, très peu de points suffisent, dans d'autres cas, il faut calculer beaucoup de points. Il est toujours nécessaire de réfléchir.
Quand ton graphique correspond au résultat demandé, passe à la page suivante.
